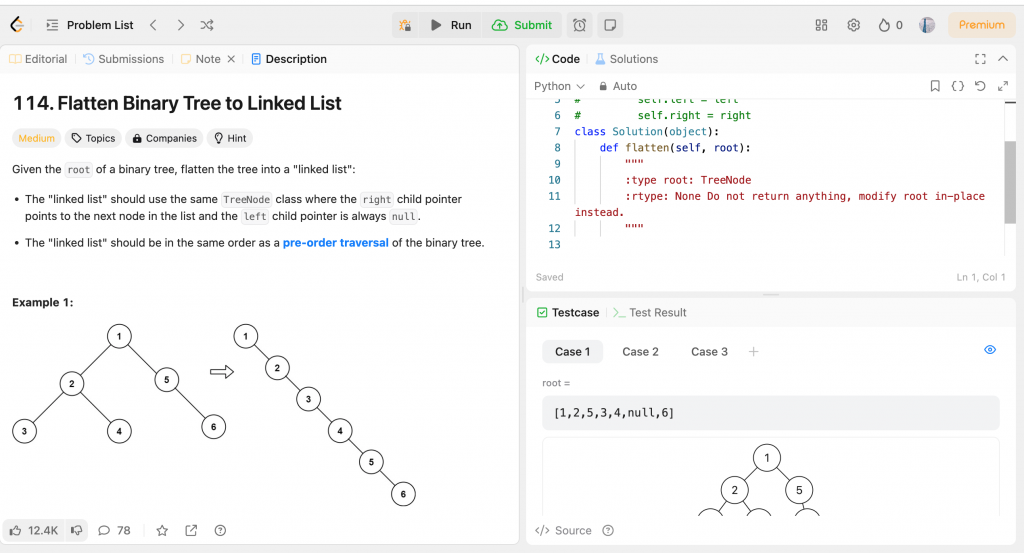
這題要把給定的二元樹扁平化（flatten），讓它像一個單向鏈表，主要是讓樹的右指標指向鏈表中的下個節點，左指標設為成null，這個“鏈表”須遵依照原來樹的先序遍歷順序，就是先根、再左子樹、最後右子樹這個順序。

想法：
先序遍歷順序是根-左-右，這是我要建的順序，就是在轉為鏈表後，根節點會排在最前面，然後是左子樹中的節點，最後才是右子樹，用遞迴處理，從根節點開始，遞迴處理它的左子樹和右子樹，先把左子樹扁平化，然後把右子樹拼到左子樹的最右，最後讓右指標指向這個拼好的鏈表，也可以用迭代法處理，避免用遞迴消耗額外空間，在每個節點上，如果它有左子樹，就把左子樹插到右子樹的位置，再把原本的右子樹移到左子樹的最右邊，就地修改樹結構，重點是，這題要就地修改樹的結構，不能用額外的空間，所以要確保在修改時不會用多餘的空間。

程式碼：
#Definition for a binary tree node.
#class TreeNode(object):
#def init(self, val=0, left=None, right=None):
#self.val = val
#self.left = left
#self.right = right

class Solution(object):
def flatten(self, root):
"""
:type root: TreeNode
:rtype: None Do not return anything, modify root in-place instead.
"""
if not root:
return

    #定義一個指針指向當前節點
    current = root
    
    while current:
        # 如果左子樹不是空，處理左子樹
        if current.left:
            # 找到左子樹的最右邊的節點
            rightmost = current.left
            while rightmost.right:
                rightmost = rightmost.right
            
            #把右子樹接到左子樹的最右邊節點的右子樹
            rightmost.right = current.right
            
            #把左子樹移到右邊
            current.right = current.left
            current.left = None
        
        #繼續處理下一個節點
        current = current.right

解釋：
遍歷每個節點，從 current 開始把根節點指向 root，每次檢查當前節點是不是有左子樹，找到左子樹的最右節點，在有左子樹的情況要找到那顆左子樹的最右節點，因為它就是右子樹的連接點，重新排子樹把當前節點的右子樹連到左子樹的最右節點，然後把左子樹移到右邊，左指標設為 null，繼續遍歷右子樹，最後移到右子樹繼續執行這個過程，直到整個樹扁平化，網上查到這是一個 in-place 的解法，不用額外的記憶體空間，且有效地保持先序遍歷的順序。

步驟：
遍歷每個節點，從根節點開始，檢查當前節點的左子樹，把左子樹接到右子樹，如果左子樹存在，把左子樹的最右邊節點找到，再把原本的右子樹接到該節點的右子樹位置，移動左子樹把左子樹放到右子樹的位置，再把左子樹設為成null，繼續處理，移動到下一個右子樹，直到整棵樹遍歷完。

心得：
這題考對二元樹的理解，尤其是先序遍歷和二元樹結構的運用，在程設上，要熟悉指針操作，因為要就地修改二元樹的結構，這關係到對指針的精準處理，過程中處理左子樹的遷移時是關鍵要確保不會因為指針錯誤導致鏈表結構混亂，另外控制程式的時間與空間複雜度這個能力我也越來越熟悉，這題用原地修改來避免額外空間的消耗，對優化程式性能很重要。